This one week summer school belongs to the PSL-maths program of the PSL university. It is devoted to High dimensional probability and algorithms. The targeted audience is young and less young mathematicians, starting from the PhD level. The school will take place in ÉNS Paris, from July 1 to 5, 2019.

• Venue. Amphi Rataud, École Normale Supérieure, 45 rue d'Ulm, Paris (Maps, Street view, ÉNS map)
• Program and practical details. (PDF)
• Registration. Free but mandatory
• Format. The school will consist in...
  • one 9-hour course by Sébastien Bubeck (Microsoft Research)
  • one 9-hour course by Joel Tropp (California Institute of Technology)
  • six 45-minute talks by
    • Yohann De Castro (École des Ponts)
    • Alexandra Carpentier (U. Potsdam)
    • Olga Klopp (ESSEC / CREST)
    • Laurent Massoulié, (INRIA/Microsoft)
    • Nicolas Verzelen (INRA)
    • Lenka Zdeborova (CNRS / CEA Saclay)

• Wifi. Eduroam or ask the organizers for a special account
• Coffee breaks. in Espace Cartan – Maths department (DMA)
• Wednesday Buffet. in the restaurant « patio » or in « Cour Pasteur » if nice weather
• Lunches. Not provided. 
• List of restaurants. (PDF)
• Bakeries map. (PNG)
• Group photo. (JPG)
• The video capture of the courses and talks are available on Canal-U.

• Bubeck - Some geometric aspects of randomized online decision making. This course will be concerned with some of the canonical non-stochastic models of online decision making. These models have their origin in works from the 1950's and 1960's, and went through a resurgence in the mid-2000's due to many applications in the internet economy. This course will focus on a set of challenging conjectures around these models from the 1980's and 1990's. We will present a unified approach based on a combination of convex optimization techniques together with powerful probabilistic tools, which will allow us to derive state of the art results in online learning, bandit optimization, as well as some classical online computing problems (k-server and metrical task systems). Special emphasis will be given to proper introduction of the mathematical/algorithmic tools: gradient descent, mirror descent (i.e., Riemannian gradient descent), probabilistic embedding of metric spaces, some basic results in convex geometry, etc. 
  • Draft lecture notes: PDF
  • Video capture: 1 2 3 4 5 6 7 8 9
    
• Tropp - Random matrix theory and computational linear algebra. This course will treat some contemporary algorithms from computational linear algebra that involve random matrices. Rather than surveying the entire field, we will focus on a few algorithms that are both simple and practically useful. We begin with an introduction to matrix concentration inequalities, which are a powerful tool for analyzing structured random matrices. We will use these ideas to study matrix approximations constructed via randomized sampling, such as the random features method. As a more sophisticated application, we will present a complete treatment of a recent algorithm for solving graph Laplacian linear systems in near-linear time. Some references : 1. Tropp, "An introduction to matrix concentration inequalities," Found. Trends. Mach. Learning, 2015. 2. Kyng, "Approximate Gaussian elimination," PhD Thesis, Yale, 2017. 3. Tropp, "Matrix concentration and computational linear algebra," ACM technical report 2019-01, Caltech, Pasadena, 2019.  
  • Draft lecture notes: PDF
  • Video capture: 1 2 3 4 5 6 7 8 9
    
• De Castro - Spectral convergence of random graphs and a focus on random geometric graphs. In this talk, we present a non-asymptotic bound on the L2 distance between the spectrum of the probability matrix of a random graph and the spectrum of the integral operator. Then, we study the random geometric graph model and we show how to adaptively estimate the graphon and the gram matrix of the latent points in this case.
  
  • Video capture: 1
• Carpentier - Introduction to some problems of composite and minimax hypothesis testing.  A fundamental question in statistics is: how well can we fulfil a given aim given the data that one possesses? Answering this question sheds light on the possibilities, but also on the fundamental limitations, of statistical methods and algorithms. In this talk, we will consider some examples of this question and its answers in the hypothesis testing setting. We will consider the Gaussian model in (high) dimension p where the data are of the form X = \theta + \sigma \epsilon, where \epsilon is a standard Gaussian vector with identity covariance matrix.  An important hypothesis testing question consists in deciding whether \theta belongs to a given subset \Theta_0 of R^p (null hypothesis) or whether the l_2 distance between \theta and the set \Theta_0 is larger than some quantity \rho (alternative hypothesis). We will investigate how difficult, or easy, this testing problem is, namely how large \rho has to be so that the testing problem has a meaningful solution - i.e. that a non-trivial tests exists. We will see through several examples that the answer to this question depends on the shape of \Theta_0 in an interesting way.
  • Video capture : 1
• Klopp - Sparse Network Estimation. Inhomogeneous random graph models encompass many network models such as stochastic block models and latent position models. We consider the problem of the statistical estimation of the matrix of connection probabilities based on the observations of the adjacency matrix of the network. We will also discuss the problem of graphon estimation when the probability matrix is sampled according to the graphon model. For these two problems, the minimax optimal rates of convergence in Frobenius norm are achieved by the least squares estimator which is known to be NP-hard. In this talk we will present two alternatives to the least squares: the hard thresholding estimator and the maximum likelihood estimator. We will provide new results for these two methods. We will also discuss the problem of link prediction commonly encountered in applications.
  • Slides : PDF
    
  • Video capture: 1
• Massoulié - Planting trees in graphs, and finding them back. In this talk we  consider detection and reconstruction of planted structures in Erdős-Rényi random graphs. For planted line graphs, we establish the following phase diagram. In a low density region where the average degree λ of the initial graph is below some critical value λc, detection and reconstruction go from impossible to easy as the line length K crosses some critical value f(λ)ln(n), where n is the number of nodes in the graph. In the high density region λ>λc, detection goes from impossible to easy as K goes from o(\sqrt{n}) to ω(\sqrt{n}), and reconstruction remains impossible so long as K=o(n). We show similar properties for planted D-ary trees. These results are in contrast with the corresponding picture for detection and reconstruction of low rank planted structures, such as dense subgraphs and block communities: We observe a discrepancy between detection and reconstruction, the latter being impossible for a wide range of parameters where detection is easy. This property does not hold for previously studied low rank planted structures.
  • Slides : PPT
  • Video capture: 1
• Verzelen - Clustering with the relaxed K-means. This talk is devoted to clustering problems. It amounts to partitionning a set of given points or the nodes of a given graph, in such a way that the groups are as homogeneous as possible. After introducing two random instances of this problem, namely sub-Gaussian Mixture Model (sGMM) and Stochastic Block Model (SBM), I will explain how convex relaxations of the classical $K$-means criterion achieve near optimal performances. Emphasis will be put on the connections between the clustering bounds and relevant results in random matrix theory.
  • Slides : PDF
  • Video capture: 1
• Zdeborova - Loss landscape and behaviour of algorithms in the spiked matrix-tensor model. A key question of current interest is: How are properties of optimization and sampling algorithms influenced by the properties of the loss function in noisy high-dimensional non-convex settings? Answering this question for deep neural networks is a landmark goal of many ongoing works. In this talk I will answer this question in unprecedented detail for the spiked matrix-tensor model. Information theoretic limits, and Kac-Rice analysis of the loss landscapes, will be compared to the analytically studied performance of message passing algorithms, of the Langevin dynamics and of the gradient flow. Several rather non-intuitive results will be unveiled and explained. 
  
  • Video capture: 1

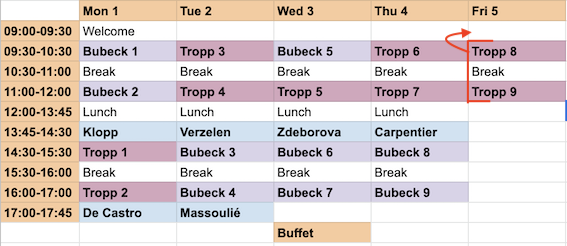
Schedule (check this site for updates!). Note that lunches are not provided by the organization.

Registration is free but mandatory. Some limited support is available for young participants.

The deadline for registration is April 1, 2019.

Registration may close before if the number of registered persons exceeds the capacity of the room.

This school is supported by PSL-maths, a program of the PSL university. It is additionally supported by CNRS. 

The organizers are Claire Boyer, Djalil Chafaï, and Joseph Lehec.

The video capture was produced technically by Thierry Bohnke and Marianne Herve from OHNK.